今天來聊聊B-tree吧!
B-tree是一種高效的資料結構,特別適用於處理大量資料和優化I/O操作。它常用於多存儲系統中,特別是磁盤存儲和數據庫系統,以確保高效的數據組織和查詢。以下是B-tree的一些重要特點和操作:
B樹的所有葉子節點都處於相同的層級,這有助於保持平衡並簡化查詢。
B樹的結構由一個稱為「最小度」的參數t來定義,該參數通常取決於磁碟區塊的大小。
每個節點的子節點數等於該節點中的鍵數加1,這有助於保持平衡。
節點的所有鍵按升序排序,這使得範圍查詢變得容易,並提供高效的查詢操作。
B樹是一個自我平衡的結構,可以在需要時生長或收縮。與二元搜尋樹不同,B樹可以向上或向下調整以保持平衡。
與 Binary Tree Search 相似,只是要比 多個鍵值。
Node *BTree :: search(Node *r , char k){
int i = 0;
while(i < r->n && k > r->key[i]) // 左到右找
i++;
if(i < r->n && k == r->key[i]) // 找到
return r;
if(r->leaf) // 已經是葉節點
return NULL;
else
return search(r->child[i],k); // 遞迴找
}
將一個新的鍵值(key)插入B-tree中的操作。插入操作通常遵循以下步驟:
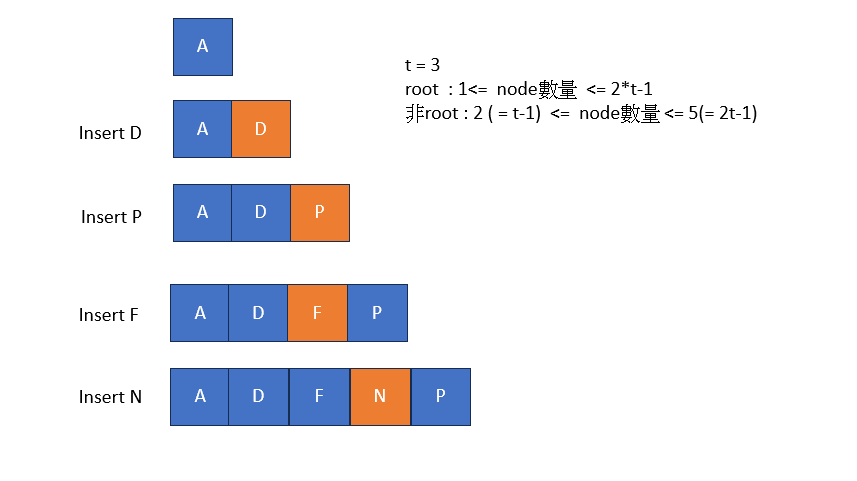
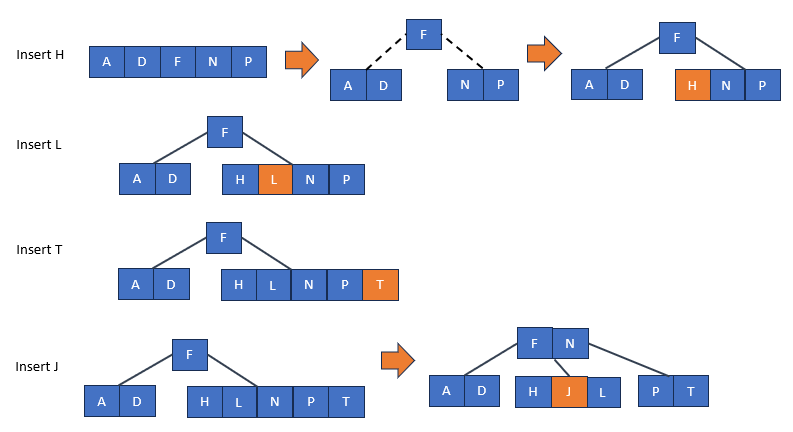
將中間的鍵值提升到父節點
void BTree :: splitChild(Node *r,int i,Node *y){
// y的第MAX_KEYS/2個鍵值會上升到y的父節點
Node *z = new Node(y->leaf); // 建立新節點
z->n = MAX_KEYS/2; // 新節點的鍵值數量
// 複製鍵值
for(int j = 0 ; j < MAX_KEYS/2 ; j++) // 複製鍵值
z->key[j] = y->key[j+MAX_KEYS/2+1];
if(!y->leaf){ // 如果不是葉節點
for(int j = 0 ; j <= MAX_KEYS/2 ; j++) // 複製子節點
z->child[j] = y->child[j+MAX_KEYS/2+1];
}
y->n = MAX_KEYS/2; // y的鍵值數量
for(int j = r->n ; j >= i+1 ; j--) // 往後移動
r->child[j+1] = r->child[j];
r->child[i+1] = z; // 將新節點插入到父節點
for(int j = r->n-1 ; j >= i ; j--) // 往後移動
r->key[j+1] = r->key[j];
r->key[i] = y->key[MAX_KEYS/2]; // 將y的第MAX_KEYS/2個鍵值上升到父節點
r->n++;
}
void BTree ::insertNonFull(Node *r,char k){ // 已知沒有滿
int i = r->n-1; // 最後一個鍵值的索引
if(r->leaf){ // 如果是葉節點
while(i >= 0 && k < r->key[i]){ // 找到插入位置
r->key[i+1] = r->key[i];
i--;
}
r->key[i+1] = k;
r->n++;
}
else{ // 如果不是葉節點
while(i >= 0 && k < r->key[i]) // 找到插入位置
i--;
i++;
if(r->child[i]->n == MAX_KEYS){ // 如果子節點已滿
splitChild(r,i,r->child[i]); // 分裂子節點
if(k > r->key[i])
i++;
}
insertNonFull(r->child[i],k); // 遞迴插入
}
}
void BTree :: insert(char k){
if(root == NULL){ // 如果是空樹
root = new Node(k);
}
else{
if(root->n == MAX_KEYS){ // 如果根節點已滿
Node *s = new Node(false); // 建立新的根節點
s->child[0] = root;
splitChild(s,0,root); // 分裂根節點
int i = 0;
if(s->key[0] < k)
i++;
insertNonFull(s->child[i],k); // 遞迴插入
root = s;
}
else
insertNonFull(root,k); // 遞迴插入
}
}
刪除操作相對於插入而言更為複雜,這是因為我們可以從任何節點(而不僅僅是葉子節點)刪除鍵值,同時,當我們從內部節點刪除鍵值時,必須重新排列該節點的子節點,同時確保不違反B樹的屬性。以下是B-tree刪除操作的基本步驟: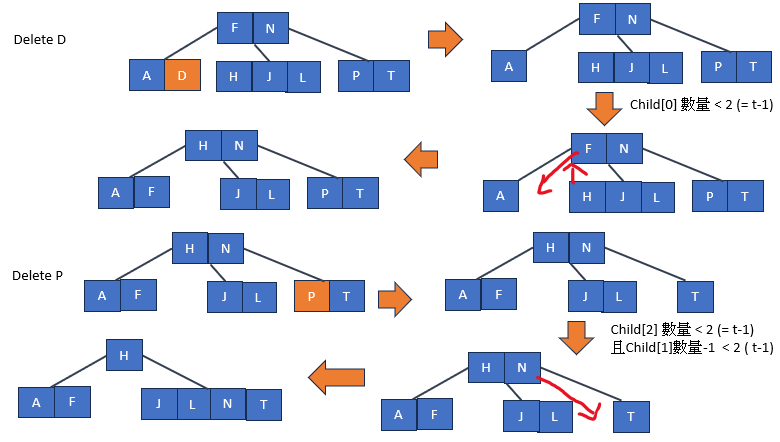
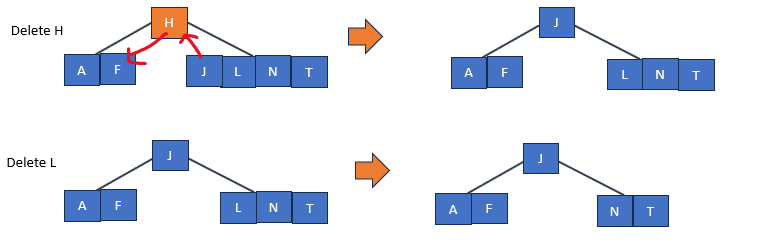
如上圖操作,我們處理三種可能的情況:
處理葉子節點情況: 如果目標節點是葉子節點(即沒有子節點)刪除,如果該葉子節點的鍵值數量少於最小度t-1(即t-1個鍵值),這就需要進行一些額外的操作,以確保B-tree的平衡性和性質仍然得以保持。
以下是處理這種情況的一般步驟:
void BTree :: borrowFromPrev(Node *r,int idx){ // 從左邊借
Node *child = r->child[idx];
Node *sibling = r->child[idx-1];
for(int i = child->n-1 ; i >= 0 ; i--) // 往後移動
child->key[i+1] = child->key[i];
if(!child->leaf){ // 如果不是葉節點
for(int i = child->n ; i >= 0 ; i--) // 往後移動
child->child[i+1] = child->child[i];
}
child->key[0] = r->key[idx-1]; // 從父節點借一個鍵值
if(!child->leaf) // 如果不是葉節點
child->child[0] = sibling->child[sibling->n]; // 從左邊的子節點借一個子節點
r->key[idx-1] = sibling->key[sibling->n-1]; // 從左邊的子節點借一個鍵值
child->n++;
sibling->n--;
}
void BTree :: borrowFromNext(Node *r,int idx){ // 從右邊借
Node *child = r->child[idx]; // 子節點
Node *sibling = r->child[idx+1]; // 兄弟節點
child->key[child->n] = r->key[idx]; // 從父節點借一個鍵值
if(!child->leaf) // 如果不是葉節點
child->child[child->n+1] = sibling->child[0]; // 從右邊的子節點借一個子節點
r->key[idx] = sibling->key[0]; // 從右邊的子節點借一個鍵值
for(int i = 1 ; i < sibling->n ; i++) // 往前移動
sibling->key[i-1] = sibling->key[i];
if(!sibling->leaf){ // 如果不是葉節點
for(int i = 1 ; i <= sibling->n ; i++) // 往前移動
sibling->child[i-1] = sibling->child[i];
}
child->n++;
sibling->n--;
}
void BTree :: merge(Node *r,int idx){ // 合併子節點
Node *child = r->child[idx];
Node *sibling = r->child[idx+1];
child->key[t-1] = r->key[idx]; // 從父節點借一個鍵值
for(int i = 0 ; i < sibling->n ; i++) // 複製鍵值
child->key[i+t] = sibling->key[i];
if(!child->leaf){ // 如果不是葉節點
for(int i = 0 ; i <= sibling->n ; i++) // 複製子節點
child->child[i+t] = sibling->child[i];
}
for(int i = idx+1 ; i < r->n ; i++) // 往前移動
r->key[i-1] = r->key[i];
for(int i = idx+2 ; i <= r->n ; i++) // 往前移動
r->child[i-1] = r->child[i];
child->n += sibling->n+1;
r->n--;
}
至少有t個鍵的節點: 在這種情況下,我們需要找到目標鍵值的「替代品」。這個替代品通常是位於目標鍵值的左子樹中的最大鍵值,或者是位於右子樹的最小鍵值。我們將這個替代品鍵值複製到目標節點,然後刪除該替代品鍵值所在的子樹中的相應鍵值,從而完成了刪除操作。
具體來說,如果目標節點的左子節點至少包含t個鍵,我們可以找到左子節點中的最大鍵值來代替目標鍵值,然後遞歸地刪除最大鍵值。同樣地,如果右子節點至少包含t個鍵,我們可以找到右子節點中的最小鍵值來代替目標鍵值,然後遞歸地刪除最小鍵值。
Node* BTree :: maxTree(Node *r){ // 找到最大的鍵值
if(r->leaf)
return r;
else
return maxTree(r->child[r->n]);
}
Node* BTree :: minTree(Node *r){ // 找到最小的鍵值
if(r->leaf)
return r;
else
return minTree(r->child[0]);
}
處理節點內鍵值數不足的情況: 如果刪除操作導致某些節點的鍵值數量低於最小度t所要求的最低數量,則需要進行重新平衡操作。這可能包括向兄弟節點借鍵值,或者如果兄弟節點也具有最小鍵值數量,則合併兄弟節點以維護平衡性。刪除操作的複雜性在於它需要根據不同情況執行多個步驟,以確保B-tree的結構和性質保持完整。
void BTree :: deleteKey(Node *r,char k){
if (r == NULL)
return;
int i = 0;
while(i < r->n && k > r->key[i]) // 左到右找
i++;
if(i < r->n && k == r->key[i]){ // 找到
if (r->leaf){// 如果是葉節點
for(int j = i ; j < r->n-1 ; j++) // 往前移動
r->key[j] = r->key[j+1];
r->n--;
if(r->n == 0)
root = NULL;
if(r->n < t-1)
fill(r,i);
return;
}
else{ //不是葉節點
if(r->child[i]->n > t-1){ // 如果左邊的子節點的鍵值數量大於等於t
Node *pre = maxTree(r->child[i]); // 找到前驅
r->key[i] = pre->key[pre->n-1]; // 從前驅借一個鍵值
deleteKey(r->child[i],pre->key[pre->n-1]); // 遞迴刪除
}
else if(r->child[i+1]->n > t-1){ // 如果右邊的子節點的鍵值數量大於等於t
Node *next = minTree(r->child[i+1]); // 找到後繼
r->key[i] = next->key[0]; // 從後繼借一個鍵值
deleteKey(r->child[i+1],next->key[0]); // 遞迴刪除
}
else{ // 如果左右都沒有可以借的
merge(r,i); // 合併右邊的子節點
deleteKey(r->child[i],k); // 遞迴刪除
}
}
}
else{ //
if(r->leaf) // 如果是葉節點
return;
bool flag = false;
if(i == r->n) // 如果是最後一個子節點
flag = true;
if(r->child[i]->n < t) // 如果子節點的鍵值數量小於t
fill(r,i); // 填充子節點
if(flag && i > r->n) // 如果是最後一個子節點
deleteKey(r->child[i-1],k); // 遞迴刪除
else
deleteKey(r->child[i],k); // 遞迴刪除
}
}
總的來說,B-tree是一種非常有用的數據結構,特別適合處理大量數據和優化I/O操作,並且能夠自我平衡以維持高效性能。它在數據庫系統和文件系統中廣泛應用,用於高效地組織和查詢數據。
